背景问题

我们有时候需要处理一些 _时间序列数据_，比如 股票预测，天气预测，根据前面单词预测后续一个单词等场景。NN（Neural Network） 在处理这些问题，有他的局限性。RNN （Recurrent Neural Network），就是为了用于处理这些问题。

原理

一句话：能够记住前 X 步，离当前时间越近的，越记得深刻，即越能影响当前步的输出。

里面有几层意思：

  1. 当前步输出，与前 X 步的记忆构成
  2. 前 X 步的输入，就构成了 前 X 步的记忆
  3. 前 X 步的记忆，X 越小，权重越大，越能影响当前步的输出

和人的记忆就很像，越近的事件，当然记得越清了，越往前倒，就记得越模糊。

简单的示意图，颜色越红，就是记得越清楚的。越往后，“what” 这个单词就已经不记得了。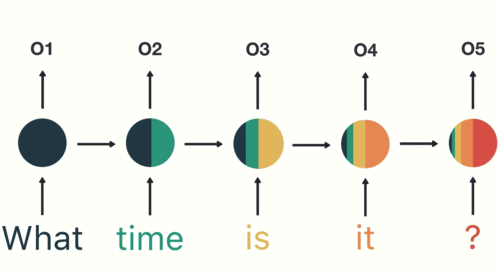

💡 所以搞清清楚 记忆，输入，输出，时间步 之间的关系，是 RNN 的关键。（NN 就没有 记忆 和 时间步 的概念）

时间步，就是表示时间序列。比如 股市指标的每秒钟时刻，天气浮动的每天时刻，一句话中的每个单词的前后顺序时刻，他们都是有先后关系的。
记忆，就好像 **每个时间步 **的一个内存，他记录着当前步的信息。我们可以使用更加专业的 隐状态（Hidden State）来表示。他随着时间步的递进，里面保存的消息慢慢弱化，直至消失。

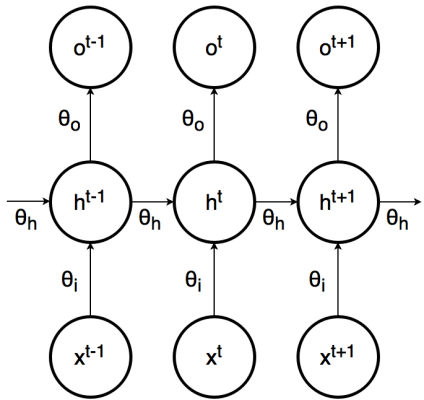
原理图

上述是 RNN 的原理图。
h: 是隐状态，x: 是输入，o: 是输出， 上面 3 个变量都是与时间步相关的，有时间标注。
图中的意思是： t 时刻的 h（隐状态），由 t-1 时刻的 h（隐状态）和 t 时刻的 x（输入）生成；t 时刻的 o（输出），由 t 时刻的 h（隐状态）生成。

总结成下面的两个公式:
$h_t = f(x_t, h_{t-1})$
$o_t = g(h_t)$

因为 又可以展开来 $[ h_{t-1} = f(x_{t-1}, h_{t-2})]$ ，且 $h_{t-2}$ 也同样展开，这样延续下去，就可以无限展开。
因为硬件限制和计算限制，我们会有 时间步 sequence 的概念，就是当前步的预测，仅仅是与前 n 步的隐状态相关，n 就是 sequence 的意思。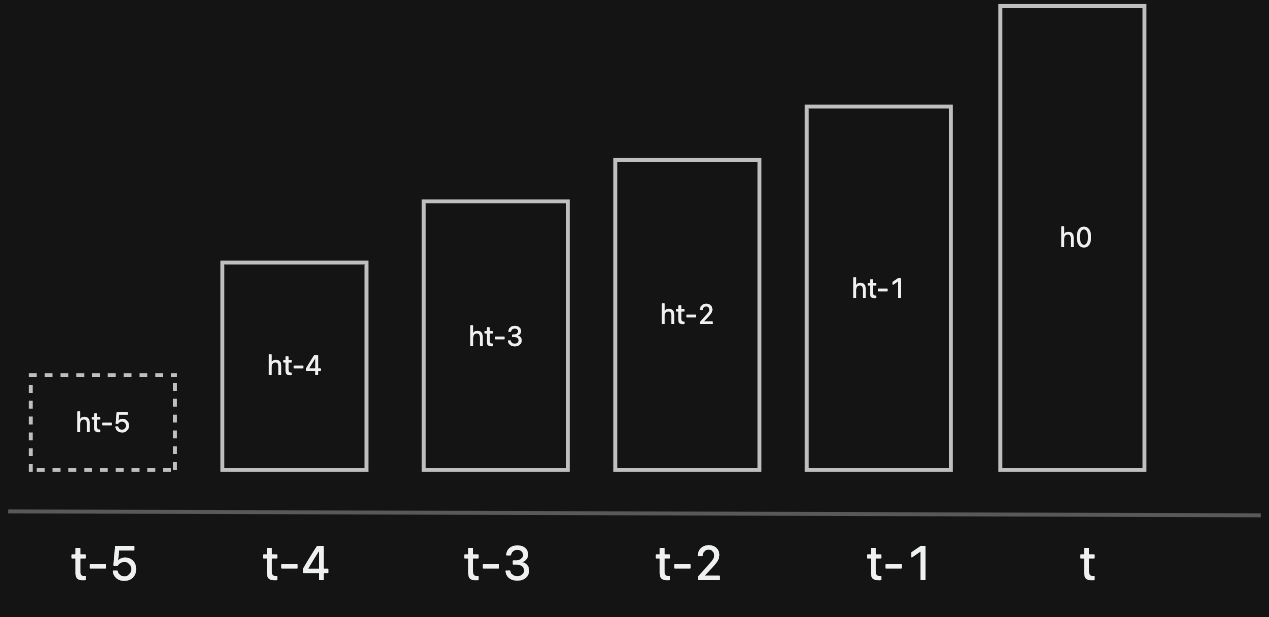
image.png
比如上图， sequence = 4， 长方形就是 隐状态，长度就是权重，越往左边，代表时间越久远，长度越矮，隐状态的权重越低。后面就会逐渐消失，所以 $h_{t-5}$ 对 $h_{t}$ 就不会再起作用了。

整体的公式非常的简单，可以记住，或者不用记忆，了解大致通俗的意思也是可以的。下面手写 RNN 的组件就把上面的公式 用代码展现出来。

手写 RNN 组件

根据上述的说明，形成 隐状态，是整个 RNN 的关键。手动实现 RNN 组件，就能了解他的内部运行机制是什么，利于理解他的原理。

手写组件 是为了对 RNN 理解更加深入，后续都使用 nn.RNN 已经封装好的方法，不再使用手写 RNN。可运行 ipynb 文件链接。

下面是模拟有 10 个时刻（ sequence 变量 ）的输入数据，从 输入 形成 _隐状态_，并且从 隐状态 生成 输出 的过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
hidden_size = 20 # 记忆体的维度
input_size = 1 # 输入特征
output_size = 1 # 输出特征


# 输入的映射关系，更新 记忆体的数据
i2h = nn.Linear(input_size + hidden_size, hidden_size)  # 输入到隐藏层
# 从 记忆体的数据 生成 输出数据
i2o = nn.Linear(hidden_size, output_size)  # 隐藏层到输出层

# 初始化一个输入，格式是就是 (sequence, input_feature)
sequence = 10
X = torch.rand(sequence,1)
# 初始化一个记忆体, sequence, feature
hidden = torch.zeros(len(X), hidden_size)

# [1] 混合 输入 和 前一个记忆体
combined = torch.cat((X, hidden), 1)  # torch.Size([1, 21])

# [2] 形成 新的记忆体
hidden = i2h(combined)
# [3] 输出 output
output = i2o(hidden)

# 后续加上 损失函数 和 优化函数 和 反向传播，就是一个完整的 RNN 的流程。

上述就是一个最简单的 RNN 组件的实现逻辑，代码简单清晰，就不再一句句说明。

有几个需要注意的地方：

  1. [1] + [2] 即是 $f(x_t , h_{t-1})$ ， torch.cat + i2h (full connect) ，输出 $h_t$当前 hidden_state 。
  2. [3] 即是 $g(h_t)$ ， i2o (hidden)，输出 $o_t$当前输出，就是从 当前hidden_state 中来
  3. 上述代码整合到一个 model 里面，循环起来，就会是一个手写 RNN。
  4. [1] 中，torch.cat((X, hidden), 1) 是 10 * input 和 hidden_state 混合建立联系；当然可以 $f(x_1, hidden_0)$; $f(x_2, hidden_1)$; $f(x_3, hidden_2)$ … $f(x_10, hidden_9)$ 逐步堆叠 hidden_state，这样会更加的直观。

例子 - 预测字符

目的：由“2 个字符”，预测下一个字符，同时连续猜测下去。
训练数据： “hello world”。

分析过程：

  1. 是 分类问题
  2. “2 个字符” 是一个有连续先后关系的输入，所以使用 RNN
  3. 定义 RNN 的时候 input_feature 和 output_feature 都是 8（字符串的所有唯一值总数是 8）
  4. X 的 sequence 可以定义成 2

详细的代码可以直接访问 ipynb 文件链接。
训练后的结果：

1
2
3
4
5
6
# 测试模型
start_str = "he"
predict_times = 5

###### output predict
# Predicted string: hello w

例子 - 预测 GS10

目的：由前 6 年数据，是否可以预测到 下一年的数据
训练数据： 美国国债收益率数据
分析过程：

  1. 是 回归问题
  2. “前 6 年数据” 预测下一年，就是有一个先后时间关系，所以使用 RNN
  3. 定义 RNN 的时候 input_feature 和 output_feature 都是 1（因为都是 数值上是 1 个值的回归）
  4. X 的 sequence 可以定义成 6

详细的代码可以直接访问 ipynb 文件链接。
训练后的结果：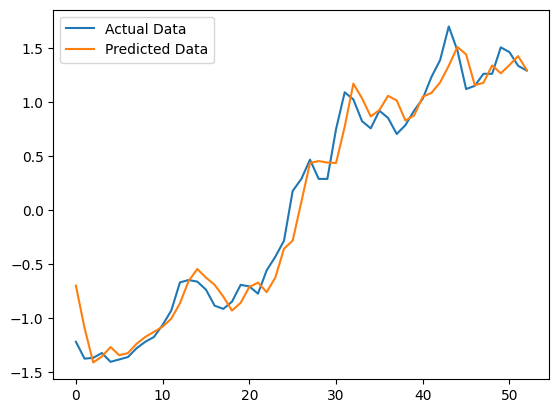
image.png

代码注意问题

集中在调用 nn.RNN 的问题

nn.RNN 的 input_feature 和 X 维度关系

在整个训练过程中，调整 model(X) 中的 X 维度，是最耗费时间的。如果语意上去理解了，那么用起来就会得心应手很多。

🔥 注意点

  1. 比如：一个 X.shape = (5,3,10)，就可以理解成 5 个样本, 3 个时间步, 每个时间步有 10 个特征
  2. X dim 至少是 2 维，分别是 (sequence, feature); 如果是 3 维，分别是 (batch, sequence, feature)；当然 也可以大于 2 维。

可运行文件链接

分类问题, X.dim = 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import torch
import torch.nn as nn

# 定义 RNN 层
# input_size 理解成 特征会比较好
rnn = nn.RNN(input_size=10, hidden_size=20, num_layers=1, batch_first=True)

# 创建输入张量 (batch_size, seq_length, input_size)
input_tensor = torch.randn(5, 3, 10)  # 5 个样本, 3 个时间步, 每个时间步有 10 个特征

# 初始化隐藏状态 (num_layers, batch_size, hidden_size)
h0 = torch.zeros(1, 5, 20)  # 1 层, 5 个样本, 每层隐藏状态有 20 个特征

# 执行前向传递
output, hn = rnn(input_tensor, h0)

# 打印输入和输出的形状
print("Input shape:", input_tensor.shape)
print("Output shape:", output.shape)
print("Hidden state shape:", hn.shape)
'''
Input shape: torch.Size([5, 3, 10])
Output shape: torch.Size([5, 3, 20])
Hidden state shape: torch.Size([1, 5, 20])
'''

同样是 rnn 的 model, X.dim = 2，一样可以运行，那么他就代表了 (seq_length, input_size)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 创建输入张量 (seq_length, input_size)
input_tensor = torch.randn(3, 10)  # 3 个时间步, 每个时间步有 10 个特征

# 初始化隐藏状态 (num_layers, batch_size, hidden_size)
h0 = torch.zeros(1, 20)  # 1 层, 5 个样本, 每层隐藏状态有 20 个特征

# 执行前向传递
output, hn = rnn(input_tensor, h0)
print("Input shape:", input_tensor.shape)
print("Output shape:", output.shape)
print("Hidden state shape:", hn.shape)

'''
Input shape: torch.Size([3, 10])
Output shape: torch.Size([3, 20])
Hidden state shape: torch.Size([1, 20])
'''

回归问题，X.dim = 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 回归的时候，基本上 1 个特征输入，1 个特征输出
import torch
import torch.nn as nn

# 定义 RNN 层
# input_size 理解成 特征会比较好
rnn = nn.RNN(input_size=1, hidden_size=20, num_layers=1, batch_first=True)

# 创建输入张量 (batch_size, seq_length, input_size)
input_tensor = torch.randn(5, 3, 1)  # 5 个样本, 3 个时间步, 每个时间步有 1 个特征

# 初始化隐藏状态 (num_layers, batch_size, hidden_size)
h0 = torch.zeros(1, 5, 20)  # 1 层, 5 个样本, 每层隐藏状态有 20 个特征

# 执行前向传递
output, hn = rnn(input_tensor, h0)

# 打印输入和输出的形状
print("Input shape:", input_tensor.shape)
print("Output shape:", output.shape)
print("Hidden state shape:", hn.shape)

'''
Input shape: torch.Size([5, 3, 1])
Output shape: torch.Size([5, 3, 20])
Hidden state shape: torch.Size([1, 5, 20])
'''

这里的 output 需要经过一个全连接层，才最后转换成真正的 output。比如下面的代码，利用上面的回归例子，模拟 output_size =1 进行输出。

1
2
3
4
5
6
7
8
9
10
11
12
#因为 RNN 层是没有 output_size,手动添加一个用于 output_size，比如回归输出 1 个特征

# 20个特征里面，提取一个输出
out_linear = nn.Linear(in_features=20, out_features=1)
output2 = out_linear(output)
print("Output shape:", output2.shape)

# 与 input 对应起来了，就是 # 5 个样本, 3 个时间步, 每个时间步有 1 个特征
'''
Output shape: torch.Size([5, 3, 1])
'''

nn.RNN 的 target 与 y 的数据的处理

还是上述的例子，回归问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 回归的时候，基本上 1 个特征输入，1 个特征输出
import torch
import torch.nn as nn

# 定义 RNN 层
# input_size 理解成 特征会比较好
rnn = nn.RNN(input_size=1, hidden_size=20, num_layers=1, batch_first=True)

# 创建输入张量 (batch_size, seq_length, input_size)
input_tensor = torch.randn(5, 3, 1)  # 5 个样本, 3 个时间步, 每个时间步有 1 个特征

# 初始化隐藏状态 (num_layers, batch_size, hidden_size)
h0 = torch.zeros(1, 5, 20)  # 1 层, 5 个样本, 每层隐藏状态有 20 个特征

# 执行前向传递
output, hn = rnn(input_tensor, h0)

# 打印输入和输出的形状
print("Input shape:", input_tensor.shape)
print("Output shape:", output.shape)
print("Hidden state shape:", hn.shape)
'''
Input shape: torch.Size([5, 3, 1])
Output shape: torch.Size([5, 3, 20])
Hidden state shape: torch.Size([1, 5, 20])
'''


#因为 RNN 层是没有 output_size,手动添加一个用于 output_size，比如回归输出 1 个特征

# 20个特征里面，提取一个输出
out_linear = nn.Linear(in_features=20, out_features=1)
output2 = out_linear(output)
print("Output shape:", output2.shape)

# 与 input 对应起来了，就是 # 5 个样本, 3 个时间步, 每个时间步有 1 个特征
'''
Output shape: torch.Size([5, 3, 1])
'''

因为训练数据 X.shape = torch.Size([5, 3, 1]) 5 个样本, 3 个时间步, 每个时间步有 1 个特征，得到 output 都是 shape 与 X 一致，都是 torch.Size([5, 3, 1])。 但是我们仅仅是需要 最后时间步 的数据，才是我们想要的数据，即 output[:, -1, :] 就是我们想要的数据。

1
2
3
4
5
6
7
8
9
10
11
#因为 RNN 层是没有 output_size,手动添加一个用于 output_size，比如回归输出 1 个特征

# 20个特征里面，提取一个输出
out_linear = nn.Linear(in_features=20, out_features=1)
output2 = out_linear(output[:,-1,:])
print("Output shape:", output2.shape)

# 与 input 对应起来了，就是 # 5 个样本, 3 个时间步, 每个时间步有 1 个特征
'''
Output shape: torch.Size([5, 1])
'''

output[:, -1, :] 取 最后时间步 的数据。这是一种取巧的方法。

但是有时候，他并不是输出最后时间步的数据，所以记得留意构建 target（真实值） 的时候，注意是否从 model 出来的 y（预测值） 的维度之间的差异。

总结

隐状态

他是一个中间状态，介于输入和输出之间，或者说记忆力，他是 RNN 的一个关键概念。
他在后续的 decode&encode 的模型中，都发挥着重要的作用。

优点和场景

序列数据的任务适合使用 RNN。

  1. 股票预测
  2. 自然语言处理

缺点

  1. 时间步过长，会导致前面的隐状态会给忘记了
  2. 梯度消失和梯度爆炸
  3. 计算效率相对比较低